Circular Intersections

How I started this problem

One day I was writing my school HW where I had to fill out a venn diagram contrasting the two presidential candidates(of the US). Because the middle section was smaller than the other two in the venn diagram, it soon ran out of space, so I thought: If I designed a venn diagram, I should make all three sections have the same area to prevent the problem. But how?

Problem

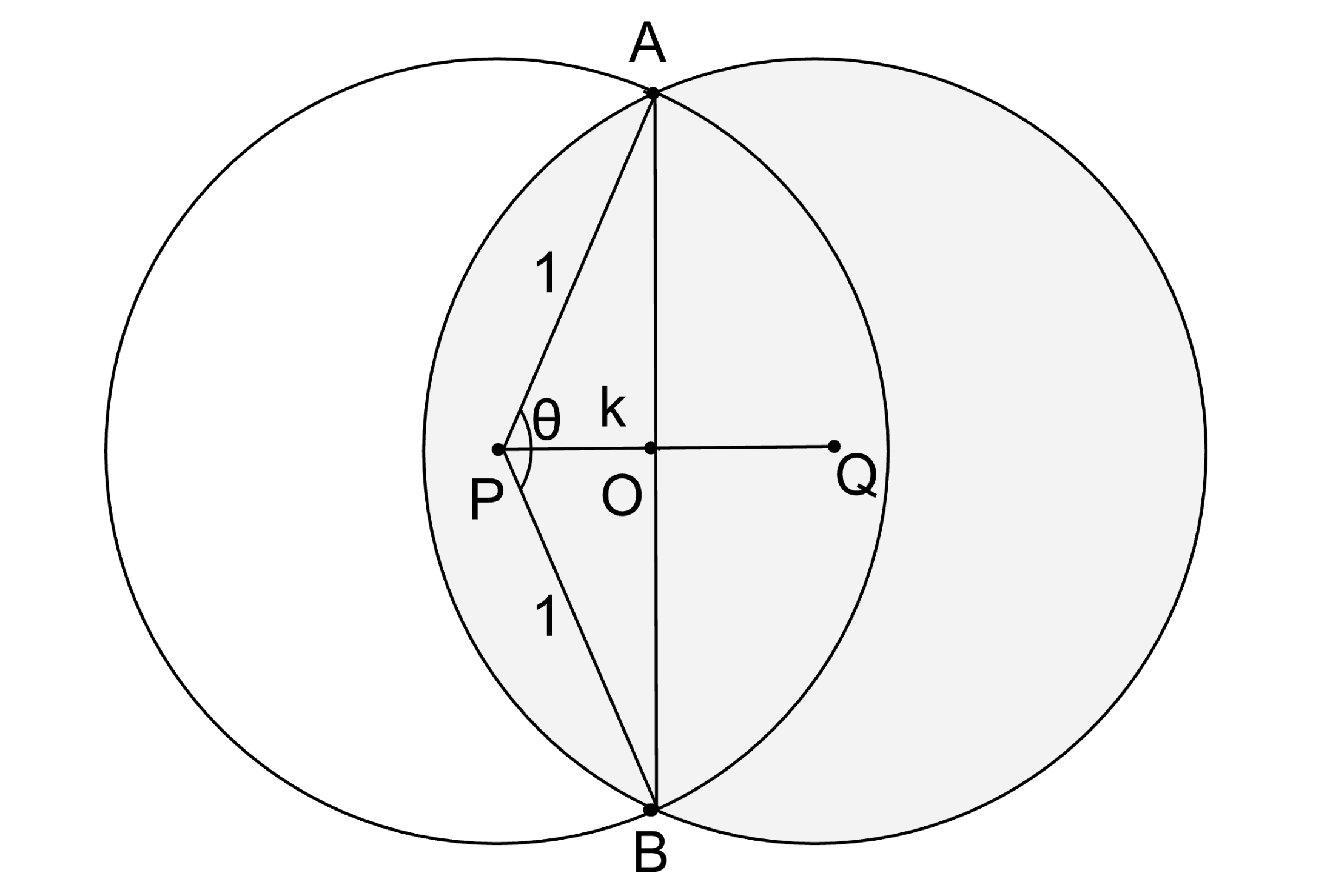
This problem is actually well defined in math. When taking two congruent circles, when are the area of the intersection of the two circles equal to the un-intersected section of one circle? Now, we start with two congruent circles of radius 1 and centers at $P$ and $Q$ respectively. The two intersection points between the circles are $A$ and $B$. Now, let the midpoint of $\overline{PQ}$ be $O$(It is also the intersection point between $\overline{PQ}$ and $\overline{AB}$). Now, denote line segment $\overline{PO}$ as $k$ and $\angle APO$ as $\theta$.

Solution

Because k is on the side adjacent to $\theta$($\angle APO$) and the hypotenuse is 1,

$$\cos (\theta )=k$$

As a result,

$$\theta =\arccos (k)$$

Let $△$ be the triangle $△$ $PAB$, it’s area is equal to $k\cdot \overline{AO}$ . By the Pythagorean thereom

$$\overline{AO}=\sqrt{1-k^2}$$

Therefore, $△=k\cdot \sqrt{1-k^2}$
Let $⌢$ equal the arc $\stackrel{⌢}{\mathrm{PAB}}$ . Because we know what $\theta$ is,

$$⌢=\frac{2\arccos (k)}{2\pi }\cdot \pi =\arccos (k)$$

Now, half of the intersection area between the two circles is equal to $⌢-△$ or

$$\arccos (k)-k\cdot \sqrt{1-k^2}$$

Thus, the full intersection area is

$$2\arccos (k)-2k\sqrt{1-k^2}$$

To check if the areas are all the same, we set the area of the circle without the intersection and the intersection

$$\pi -2\arccos (k)-2k\sqrt{1-k^2}=2\arccos (k)-2k\sqrt{1-k^2}$$

Simplifying,

$$2\arccos (k)-2k\sqrt{1-k^2}-\frac{\pi }{2}=0$$