Protoplanetary Disks
Circumstellar/Protoplanetary Disks are places where planets are spawned. In gaseous disks, solids have to grow from microscopic dust all the way up to Earth-mass planets which poses serious theoretical challenges on understanding how do they form and grow. The dynamics and evolution of the gas disks would further complicate things by interacting with the solid objects via processes such as aerodynamic drag and gravity in turbulent medium. The interaction with the disk would determine the formation of the gas giants. It might also provide observable signatures which could help us identify the proto-exoplanets.
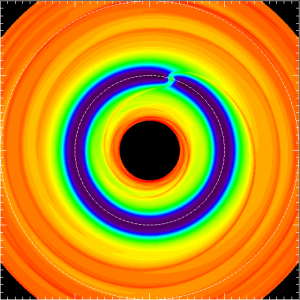Gap clearing by giant planets has been proposed to explain the optically thin cavities observed in many protoplanetary disks. How much material remains in the gap determines not only how detectable young planets are in their birth environments, but also how strong co-rotation torques are, which impacts how planets can survive fast orbital migration. We determine numerically how the average surface density inside the gap depends on planet-to-star mass ratio q, Shakura-Sunyaev viscosity parameter α, and disk aspect ratio h/r. We find the surface density contrast could easily go beyond three orders of magnitude as observed in transitional disk cavity. The scaling law shown below can be easily used to predict the planet mass given observations of disk properties (paper on ADS & astro-ph):
For Neptune mass planets:
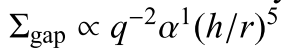
For Jupitor mass planets(this work):
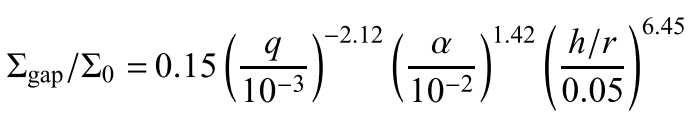
For Brown Dwarf(this work):
Protoplanetary disks which are cold and/or massive, usually when they are young, may become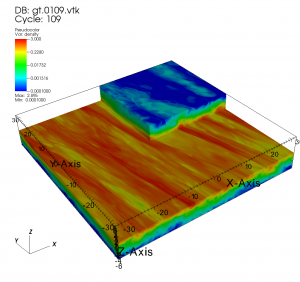 
unstable to gravitational instability. However, the unstable disks may still get away from the fatal fragmentation if the shock heating due to collapsing could not be radiated away rapidly. A self-regulated state exists when heating is balanced by cooling and is termed as “Gravito-turbulence” (Gammie 2001). To date, numerous work have been done with either 2D local/global or 3D global only simulations. And those 3D studies are mostly based on SPH simulations which are usually less accurate with shock waves and often have large numerical viscosities. On the other hand, 3D local simulation could be very useful to investigate the details of the turbulence given its higher resolution and better algorithms for handling shock heating.
We use 3D local hydrodynamic simulations of cooling,
self-gravitating disks to resolve how motions driven by “gravito-turbulence” vary with height (paper on ADS & astro-ph). We find that gravito-turbulence is practically as vigorous at altitude as at depth: even though gas at altitude is much too rarefied to be itself self-gravitating, it is strongly forced by self-gravitating overdensities at the midplane. The long-range nature of gravity means that turbulent velocities are nearly uniform vertically, increasing by just a factor of 2 from midplane to surface, even as the density ranges over nearly three orders of magnitude. The insensitivity of gravito-turbulence to height contrasts with the behavior of disks afflicted by the magnetorotational instability (MRI); in the latter case, non-circular velocities increase by at least a factor of 15 from midplane to surface, with various non-ideal effects only magnifying this factor. The distinct vertical profiles of gravito-turbulence vs. MRI turbulence may be used in conjunction with measurements of non-thermal linewidths at various depths to identify the source of transport in protoplanetary disks.
More recently, collaborating with Hirose (JAMSTEC), we made further development of this model by including realistic thermodynamics such as radiative transfer, stellar irradiation and realistic equation of state and opacity (Hirose & Shi 2017 on ADS & astro-ph). This work demonstrated the necessities of realistic thermodynamics in gravito-turbulence study and also the capability of this model to simulate realistic systems with a wide range of parameter space. Currently, we are exploring how the disk properties vary with different surface density (∼ 10-1000 g cm −2 ) at different radii (10–100 AU), and trying to map out the turbulent and fragmentation boundaries in the Σ–r phase diagram using the most realistic models to date.